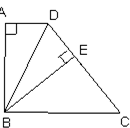
如图,长方形纸片ABCD,沿折痕AE折叠边AD,使点D落在BC边上的F处,已知AB=8,S△ABF=24,求EC的长.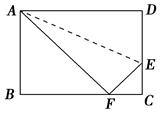
某班的学生对学校 倡导的“爱心救助”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图
倡导的“爱心救助”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图 中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的同学一共42人。
中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的同学一共42人。
(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,请你估计全校学生共捐款多少元
如图,在平面直角坐标系中,图形①与图形②关于点 成中心对称.
成中心对称.
(1)画出对称中心 ,并写出点
,并写出点 的坐标;
的坐标;
(2)将图形①向下平移4个单位,画出平移后的图形③;
(3)判断图形③与图形②是中心对称还是轴对称?
课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图,在 处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为
处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为 ,朝旗杆方向前进23米到
,朝旗杆方向前进23米到 处,再次测得旗杆顶
处,再次测得旗杆顶 端的仰角为
端的仰角为 ,求旗杆
,求旗杆
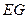 的高度.
的高度.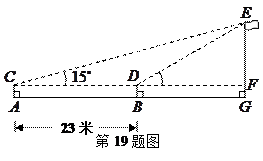
小王和小明用如图所示的同一个转盘进行“配紫色”游戏,游戏规则如下:连续转动两次转盘,如果两次转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则配成紫色)则小王得1分,否则小明得1分(如果指针恰好指在分割线上,那么重转一次,直到指针指向一种颜色为止)。
(1)请你通过列表法分别求出小王和小明获胜的概率。
(2)你认为这个游戏对双方公平吗?请说明理由:若不公平,请修改规则,使游戏对双方公平。
已知:如图,在直角梯形ABCD中,AD//BC,∠A=90°,BC=CD,BE⊥DC于点E.求证:△ABD≌△EBD