如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EG·BG=4,求BE的长.
解方程:(1)x2+5x+2=0(2)(x-5)(3x-2)="10"
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,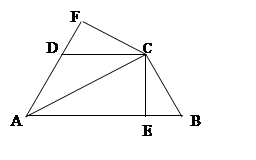
(1)试说明 .
.
(2)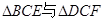 全等吗? 试说明理由.
全等吗? 试说明理由.
(3)若AC=10,CE=6, AD=5,求DF的长
(4)若AB=21,AD=9,BC=CD=10,求AC的长。
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB 长2.5米,顶端A在AC 上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?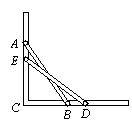
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,判断△ADE是不是等腰三角形,并说明理由。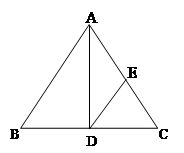
甲、乙两人参加某体育项目的训练,近期的5次测试成绩得分情况如图所示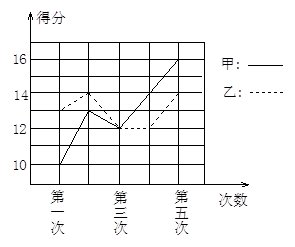
(1)分别求出2人得分的平均数与方差.
(2)根据上题算得的结果,对2人的训练成绩作出评价.