如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,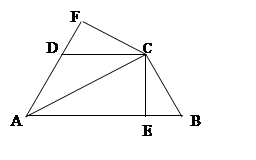
(1)试说明 .
.
(2)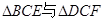 全等吗? 试说明理由.
全等吗? 试说明理由.
(3)若AC=10,CE=6, AD=5,求DF的长
(4)若AB=21,AD=9,BC=CD=10,求AC的长。
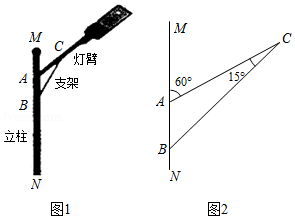
图1是某种路灯的实物图片,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于 , 两点,灯臂 与支架 交于点 ,已知 , , ,求支架 的长.(结果精确到 ,参考数据: , ,
甲、乙两人去超市选购奶制品,有两个品牌的奶制品可供选购,其中蒙牛品牌有两个种类的奶制品: .纯牛奶, .核桃奶;伊利品牌有三个种类的奶制品: .纯牛奶, .酸奶, .核桃奶.
(1)甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是 ;
(2)若甲喜爱蒙牛品牌的奶制品,乙喜爱伊利品牌的奶制品,甲、乙两人从各自喜爱的品牌中随机选购一种奶制品,请利用画树状图或列表的方法求出两人选购到同一种类奶制品的概率.
为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为 时,共分为四组: . , . , . , . ,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.

请回答下列问题:
(1)本次共调查了 名学生;
(2)请补全频数分布直方图;
(3)求扇形统计图中 组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校有多少名学生平均每天睡眠时间低于7时.
如图,在四边形 中, ,点 , 分别在 , 上, , ,求证: .

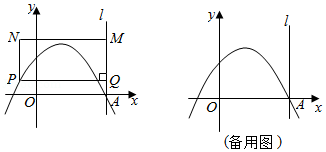
如图,在平面直角坐标系中,抛物线 与 轴正半轴交于点 ,且点 的坐标为 ,过点 作垂直于 轴的直线 . 是该抛物线上的任意一点,其横坐标为 ,过点 作 于点 , 是直线 上的一点,其纵坐标为 .以 , 为边作矩形 .
(1)求 的值.
(2)当点 与点 重合时,求 的值.
(3)当矩形 是正方形,且抛物线的顶点在该正方形内部时,求 的值.
(4)当抛物线在矩形 内的部分所对应的函数值 随 的增大而减小时,直接写出 的取值范围.