类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若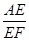 =3,求
=3,求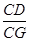 的值.
的值.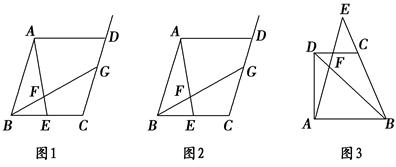
(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是________,
CG和EH的数量关系是________,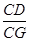 的值是________.
的值是________.
(2)类比延伸:
如图2,在原题条件下,若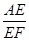 =m(m>0)则
=m(m>0)则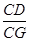 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移:
如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若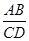 =a,
=a,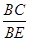 =b(a>0,b>0)则
=b(a>0,b>0)则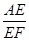 的值是________(用含a、b的代数式表示).
的值是________(用含a、b的代数式表示).
(本题10分)如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q.记△AEF的面积为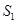 ,四边形EFQP的面积为
,四边形EFQP的面积为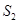 ,四边形PQCB的面积为
,四边形PQCB的面积为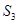
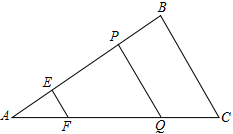
(1)求证:EF+PQ=BC
(2)若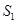 +
+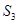 =
=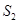 ,求
,求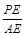 的值
的值
(3)若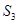 -
-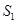 =
=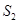 ,直接写出
,直接写出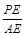 的值
的值
(本题8分)已知锐角△ABC中,边BC长为12,高AD长为8
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K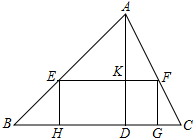
①求 的值
的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB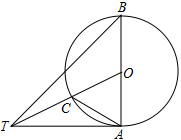
(1)求证:AT是⊙O的切线
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC的值
(本题8分),如图,已知点A(-4,2)B(-1,-2),□ABCD的对角线交于坐标原点O
(1)请直接写出点C、D的坐标
(2)写出从线段AB到线段CD的变换过程
(3)直接写出□ABCD的面积
(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4
(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率
(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:
① 两次取出的小球一个标号是1,另一个标号是2的概率
② 第一次取出标号是1的小球且第二次取出标号是2的小球的概率