一盒中有9个正品和3个次品零件,每次取一个零件,如果取出的是次品不再放回,求在取得正品前已取出的次品数X的概率分布,并求P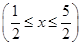 .
.
若数列{an}是等比数列,a1>0,公比q¹1,已知lna1和2+ lna5的等差中项为lna2,且a1a2 = e
(1)求{an}的通项公式;(2)设bn=  (nÎN*),求数列{bn}的前n项和.
(nÎN*),求数列{bn}的前n项和.
.已知函数 ,在点
,在点 处的切线方程
处的切线方程
为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若对于区间 上任意两个自变量的值
上任意两个自变量的值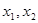 ,都有
,都有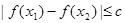 ,求实数
,求实数 的最小值;
的最小值;
(III)若过点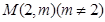 ,可作曲线
,可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围
的取值范围
(本小题满分12分).已知椭圆的中心在原点,焦点在 轴上,离心率
轴上,离心率 ,一
,一
条准线的方程为 (Ⅰ)求椭圆的方程;(Ⅱ)设
(Ⅰ)求椭圆的方程;(Ⅱ)设 ,直线
,直线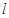 过椭圆的右焦点为
过椭圆的右焦点为
且与椭圆交于 、
、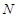 两点,若
两点,若
 ,求直线
,求直线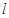 的方程
的方程
(本小题满分12分).设正项数列 的前
的前 项和为
项和为 ,满足
,满足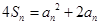 ,
,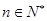 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设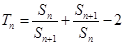 ,证明:
,证明:
(本小题满分12分).如图,在直角梯形 中,
中,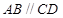 ,
, ,且
,且 ,现以
,现以 为一边向形外作正方形
为一边向形外作正方形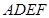 ,然后沿边
,然后沿边 将正方形
将正方形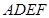 翻折,使平面
翻折,使平面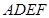 与平面
与平面 垂直,
垂直, 为
为 的中点
的中点
(I) 求证: 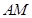 ∥平面
∥平面 ;
;
(Ⅱ)求证: 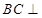 平面
平面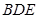 ;
;
(III) 求二面角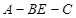 的大小.
的大小.