A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为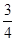 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、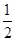 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设ξ为学生甲在三道程序中获优的次数,求ξ的分布列.
(满分15分)设函数 ,
, ,(其中
,(其中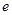 为自然底数);
为自然底数);
(Ⅰ)求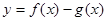 (
( )的最小值;
)的最小值;
(Ⅱ)探究是否存在一次函数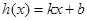 使得
使得 且
且 对一切
对一切 恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
(Ⅲ)数列 中,
中,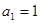 ,
,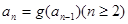 ,求证:
,求证: 。
。
(满分15分)动圆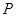 过定点
过定点 且与直线
且与直线 相切,圆心
相切,圆心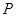 的轨迹为曲线
的轨迹为曲线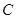 ,过
,过 作曲线
作曲线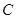 两条互相垂直的弦
两条互相垂直的弦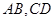 ,设
,设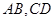 的中点分别为
的中点分别为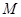 、
、 .
.
(1)求曲线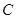 的方程;
的方程;
(2)求证:直线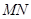 必过定点.
必过定点.
某种鲜花进价每束 元,售价每束
元,售价每束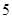 元,若卖不出,则以每束
元,若卖不出,则以每束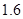 元的价格处理掉。某节日需求量
元的价格处理掉。某节日需求量 (单位:束)的分布列为
(单位:束)的分布列为
 |
200 |
300 |
400 |
500 |
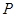 |
 |
 |
 |
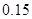 |
(Ⅰ)若进鲜花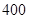 束,求利润
束,求利润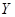 的均值。
的均值。
(Ⅱ)试问:进多少束花可使利润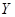 的均值最大?
的均值最大?
(满分14分)已知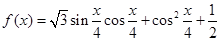 .
.
(1)求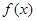 的周期及其图象的对称中心;
的周期及其图象的对称中心;
(2)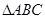 中,角
中,角 所对的边分别是
所对的边分别是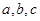 ,满足
,满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)
如图,已知椭圆 ,
,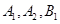 是椭圆
是椭圆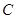 的顶点,若椭圆
的顶点,若椭圆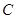 的离心率
的离心率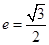 ,且过点
,且过点 .
.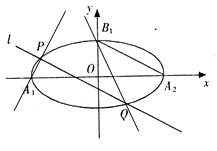
(Ⅰ)求椭圆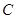 的方程;
的方程;
(Ⅱ)作直线 ,使得
,使得 ,且与椭圆
,且与椭圆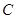 相交于
相交于 两点(异于椭圆
两点(异于椭圆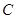 的顶点),设直线
的顶点),设直线 和直线
和直线 的倾斜角分别是
的倾斜角分别是 ,求证:
,求证: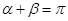 .
.