(满分15分)动圆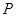 过定点
过定点 且与直线
且与直线 相切,圆心
相切,圆心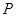 的轨迹为曲线
的轨迹为曲线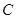 ,过
,过 作曲线
作曲线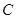 两条互相垂直的弦
两条互相垂直的弦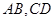 ,设
,设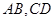 的中点分别为
的中点分别为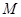 、
、 .
.
(1)求曲线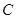 的方程;
的方程;
(2)求证:直线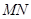 必过定点.
必过定点.
在 中,
中,
(Ⅰ)求AB的值.
(Ⅱ)求 的值.
的值.
设命题 :函数
:函数 =
= -2
-2 -1在区间(-∞,3]上单调递减;命题
-1在区间(-∞,3]上单调递减;命题 :函数
:函数 的定义域是
的定义域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求
为假命题,求 的
的 取值范围.
取值范围.
(本小题14分)
已知 ,函数
,函数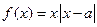 ,
, (Ⅰ)当
(Ⅰ)当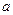 =2时,写出函数
=2时,写出函数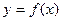 的单调递增区间;
的单调递增区间; (Ⅱ)当
(Ⅱ)当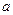 >2时,求函数
>2时,求函数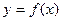 在区间
在区间 上的最小值;
上的最小值; (Ⅲ)设
(Ⅲ)设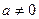 ,函数
,函数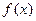 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用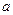 表示)
表示)
(本小题14分)
已知直线L被两平行直线 :
: 与
与 :
: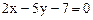 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线 上,已知
上,已知 圆
圆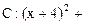
 .
.
(Ⅰ)求两平行直线 与
与 的距离;
的距离;
(Ⅱ)证明直线L与圆C恒有两个交 点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.
(本小题1 3分)
3分)
某公司要将一批不易存放的蔬菜从A地运到B 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 |
途中速度 (km/h) |
途中费用 (元/km) |
装卸时间 (h) |
装卸费用 (元) |
| 汽车 |
50 |
8 |
2 |
1000 |
| 火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B两地距离为 km
km
(I)设采用汽车与火 车运输的总费用分别为
车运输的总费用分别为 与
与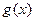 ,求
,求 与
与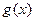 ;
;
(II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)