有一种闯三关游戏规则规定如下:用抛掷正四面体型骰子(各面上分别有1,2,3,4点数的质地均匀的正四面体)决定是否过关,在闯第n(n=1,2,3)关时,需要抛掷n次骰子,当n次骰子面朝下的点数之和大于n2时,则算闯此关成功,并且继续闯关,否则停止闯关.每次抛掷骰子相互独立.
(1)求仅闯过第一关的概率;
(2)记成功闯过的关数为ξ,求ξ的分布列.
已知椭圆 的中心在原点,它的左右两个焦点分别为
的中心在原点,它的左右两个焦点分别为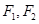 ,过右焦点
,过右焦点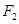 且与
且与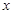 轴垂直的直线
轴垂直的直线 与椭圆
与椭圆 相交,其中一个交点为
相交,其中一个交点为
(1) 求椭圆 的方程。
的方程。
(2)设椭圆 的一个顶点为
的一个顶点为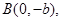 直线
直线 交椭圆
交椭圆 于另一点
于另一点 ,求
,求 的面积.
的面积.
如图所示的长方体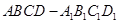 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为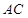 与
与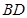 的交点,
的交点, ,
, 是线段
是线段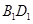 的中点.请建立空间直角坐标系解决以下问题:
的中点.请建立空间直角坐标系解决以下问题:
(1)求证: 平面
平面 ;
;
(2)求证: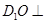 平面
平面 ;
;
(3)求二面角 的大小.
的大小.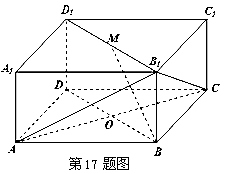
在 中,角
中,角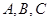 的对边分别为
的对边分别为 ,
, ,
, 的面积为
的面积为 . (1)求
. (1)求 的值;(2)求
的值;(2)求 的值.
的值.
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为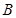 .
.
(1)求 .
.
(2)记
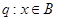 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
已知函数
(Ⅰ)求 的定义域和值域;
的定义域和值域;
(Ⅱ)写出 )的单调区间,并用定义证明
)的单调区间,并用定义证明 在所写区间上的单调性
在所写区间上的单调性