已知椭圆 的中心在原点,它的左右两个焦点分别为
的中心在原点,它的左右两个焦点分别为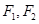 ,过右焦点
,过右焦点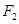 且与
且与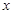 轴垂直的直线
轴垂直的直线 与椭圆
与椭圆 相交,其中一个交点为
相交,其中一个交点为
(1) 求椭圆 的方程。
的方程。
(2)设椭圆 的一个顶点为
的一个顶点为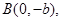 直线
直线 交椭圆
交椭圆 于另一点
于另一点 ,求
,求 的面积.
的面积.
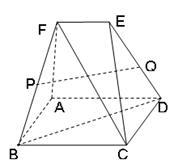
如图,多面体 中,四边形
中,四边形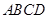 是边长为
是边长为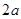 的正方形,
的正方形,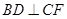 ,且
,且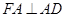 ,
, ,
,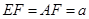 .
.
(Ⅰ)求证:平面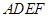 垂直于平面
垂直于平面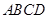 ;
;
(Ⅱ)若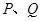 分别为棱
分别为棱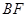 和
和 的中点,求证:
的中点,求证: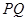 ∥平面
∥平面 ;
;
(Ⅲ)求多面体 的体积.
的体积.
数列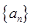 的前
的前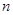 项和为
项和为 ,且
,且 .
.
(1)求数列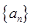 的通项公式;
的通项公式;
(2)若数列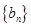 满足:
满足: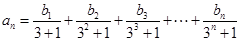 ,求数列
,求数列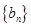 的通项公式;
的通项公式;
(3)令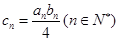 ,求数列
,求数列 的前
的前 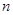 项和
项和 .
.
已知命题 :函数
:函数 在[-2,2]内有且仅有一个零点.命题
在[-2,2]内有且仅有一个零点.命题 :
: 在区间[
在区间[ ]内有解.若命题“
]内有解.若命题“ 且
且 ”是假命题,求实数
”是假命题,求实数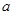 的取值范围.
的取值范围.
已知锐角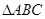 中内角
中内角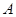 、
、 、
、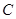 所对边的边长分别为
所对边的边长分别为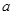 、
、 、
、 ,满足
,满足 ,且
,且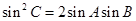 .
.
(Ⅰ)求角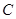 的值;
的值;
(Ⅱ)设函数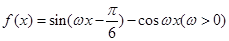 ,
, 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为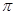 ,求
,求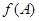 的取值范围.
的取值范围.
选修4-5:不等式选讲
已知函数 .
.
(1)求不等式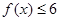 的解集;
的解集;
(2)若关于 的不等式
的不等式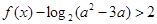 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.