数列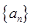 的前
的前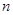 项和为
项和为 ,且
,且 .
.
(1)求数列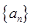 的通项公式;
的通项公式;
(2)若数列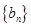 满足:
满足: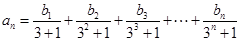 ,求数列
,求数列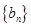 的通项公式;
的通项公式;
(3)令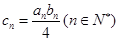 ,求数列
,求数列 的前
的前 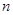 项和
项和 .
.
受日月引力的作用,海水会发生涨落,这种现象叫潮汐. 在通常情况下,船在海水涨潮时驶进航道,靠近码头,卸货后返回海洋.某港口水的深度 是时间
是时间 ,单位:
,单位: 的函数,记作:
的函数,记作: ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
经过长期观察 的曲线可以近似地看做函数
的曲线可以近似地看做函数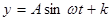 的图象.
的图象.
(Ⅰ)根据以上数据,求出函数 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时船底离海底的距离为 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
已知数列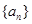 满足:
满足: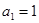 ,
,
(Ⅰ) 求证:数列 是等差数列并求
是等差数列并求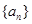 的通项公式;
的通项公式;
(Ⅱ) 设 ,求证:
,求证: .
.
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| 偏瘦 |
正常 |
肥胖 |
|
| 女生(人) |
300 |
865 |
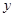 |
| 男生(人) |
 |
885 |
 |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(Ⅰ)求 的值;
的值;
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知 ,
,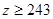 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率.
已知函数
(Ⅰ)若函数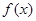 在其定义域上为单调函数,求
在其定义域上为单调函数,求 的取值范围;
的取值范围;
(Ⅱ)若函数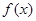 的图像在
的图像在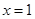 处的切线的斜率为0,
处的切线的斜率为0,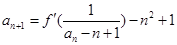 ,已知
,已知 求证:
求证:
(Ⅲ)在(2)的条件下,试比较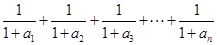 与
与 的大小,并说明理由.
的大小,并说明理由.
在直角坐标平面内,y轴右侧的一动点P到点 的距离比它到
的距离比它到 轴的距离大
轴的距离大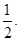
(Ⅰ)求动点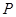 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设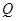 为曲线
为曲线 上的一个动点,点
上的一个动点,点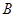 ,
, 在
在 轴上,若
轴上,若 为圆
为圆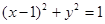 的外切三角形,求
的外切三角形,求 面积的最小值.
面积的最小值.