若a、b、c∈R+,且a+b+c=1,求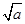 +
+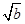 +
+ 的最大值.
的最大值.
四川省广元市2008年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2008年为累计的第一年)将首次不少于4 750万平方米?
(2)到2013年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%吗?为什么
(参考数据:1.084≈1.36,1.085≈1.47,1.086≈1.59)
已知向量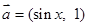 ,
, ,函数
,函数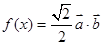 ,
,
(1)求函数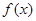 的值域;
的值域;
(2)若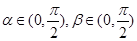 ,且
,且 ,
,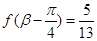 ,求
,求 的值。
的值。
在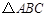 中,
中,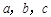 分别是三个内角
分别是三个内角 的对边.若
的对边.若 ,
, ,
,
(1)求 的值;
的值;
(2)求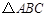 的面积
的面积 .
.
设Sn为等差数列{a n}的前n项和,已知a 9 =-2,S 8 =2.
(1)求首项a1和公差d的值;
(2)当n为何值时,Sn最大?并求出Sn的最大值.
设
(1)当 ,求
,求 的取值范围;
的取值范围;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.