(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率是0.5,购买乙种商品的概率是0.6,且购买甲种商品和购买乙种商品是相互独立的,各顾客之间购买商品也是互相独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率.
(本小题满分12分)
书桌上一共有六本不同的书.问:
(Ⅰ)6本书排成一排,要求其中的2本数学书排在一起,共有多少种不同的排法?
(Ⅱ)6本书分给甲、乙、丙三个同学,每人2本,共有多少种不同方法?
(Ⅲ)(示范性高中做)6本书分给甲、乙、丙三个同学,如果一个人得1本,一个人得2本,一个人得3本,共有多少种不同的分法?
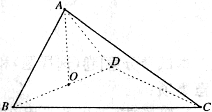
(示范性高中做)如图,四面体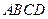 中,
中,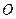 是
是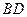 的中点,
的中点,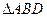 和
和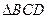 均为等边三角形,
均为等边三角形,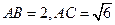 .
.
(I)求证: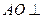 平面
平面 ;
;
(Ⅱ)求二面角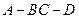 的余弦值.
的余弦值.

( 本小题满分12分)
(普通中学做)如图,四棱锥P—ABCD中,底面ABCD 为矩形,AB=8,AD=4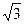 ,侧面PAD为等边三角形,并且与底面所成二面角为60
,侧面PAD为等边三角形,并且与底面所成二面角为60
求PA与底面ABCD所成角的大小.
(本小题满分10分)
已知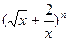 的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.
的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.