(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系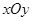 中,圆
中,圆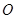 的参数方程为
的参数方程为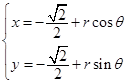 ,(
,(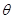 为参数,
为参数,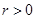 ).以
).以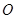 为极点,
为极点,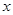 轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线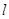 的极坐标方程为
的极坐标方程为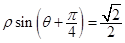 .写出圆心的极坐标,并求当
.写出圆心的极坐标,并求当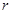 为何值时,圆
为何值时,圆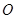 上的点到直线
上的点到直线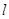 的最大距离为3.
的最大距离为3.
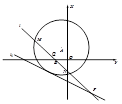
如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点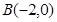 的动直线
的动直线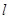 与圆
与圆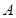 相交于
相交于 两点,
两点,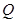 是
是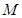 的中点,直线
的中点,直线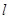 与
与 相交于点
相交于点 .
.
(1)求圆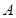 的方程;
的方程;
(2)当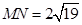 时,求直线
时,求直线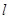 的方程;
的方程;
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
已知圆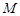 :
: ,设点
,设点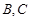 是直线
是直线 :
: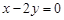 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点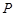 在线段
在线段 上,过
上,过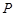 点作圆
点作圆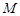 的切线
的切线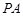 ,切点为
,切点为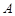 .
.
(1)若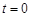 ,
,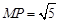 ,求直线
,求直线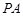 的方程;
的方程;
(2)若O为原点,经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 长的最小值
长的最小值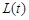 .
.
如图,已知椭圆C: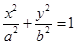 (a>b>0)的右焦点为F(c,0),下顶点为A(0,﹣b),直线AF与椭圆的右准线交于点B,若F恰好为线段AB的中点.
(a>b>0)的右焦点为F(c,0),下顶点为A(0,﹣b),直线AF与椭圆的右准线交于点B,若F恰好为线段AB的中点.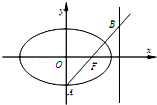
(1)求椭圆C的离心率;
(2)若直线AB与圆x2+y2=2相切,求椭圆C的方程.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
已知y=2x是△ABC中∠C的内角平分线所在直线的方程,若A(﹣4,2),B(3,1).
(1)求点A关于y=2x的对称点P的坐标;
(2)求直线BC的方程;
(3)判断△ABC的形状.