如图，已知椭圆C：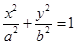
（a＞b＞0）的右焦点为F（c，0），下顶点为A（0，﹣b），直线AF与椭圆的右准线交于点B，若F恰好为线段AB的中点．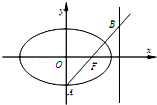
（1）求椭圆C的离心率；
（2）若直线AB与圆x2+y2=2相切，求椭圆C的方程．
（本小题满分12分）．设命题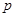
：“方程
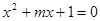有两个实数根”；命题
：“方程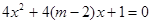
无实根”，若
为假，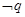
为假，求实数
的取值范围．
（本题15分）已知方程x2+y2-2（m+3）x+2（1-4m2）y+16m4+9=0表示一个圆
（1）求实数m的取值范围；
（2）求该圆半径r的取值范围；
（3）求圆心的轨迹方程。
（本题15分）已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD．
（1）求证:PF⊥FD；
（2）设点G在PA上,且EG//平面PFD,试确定点G的位置．
在正方体ABCD-A1B1C1D1中, AA1=2,E为棱CC1的中点．
（1）求三棱锥E-ABD的体积；
（2）求证：B1D1
AE；
（3）求证：AC//平面B1DE．
（本题15分）如图，ABCD是正方形，O是正方形的中心，PO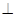
底面ABCD，E是PC的中点。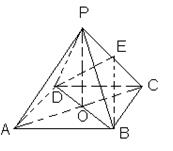
求证：（1）PA∥平面BDE
（2）平面PAC平面BDE