(本题15分)如图,ABCD是正方形,O是正方形的中心,PO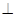 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。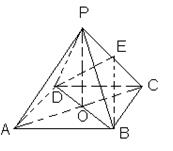
求证:(1)PA∥平面BDE
(2)平面PAC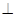 平面BDE
平面BDE
.(本小题12分)
(本小题12分)
射手张强在一次 射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24,0.28,0.19,0.16,0.13.计算这个射手在一次射击中:
射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24,0.28,0.19,0.16,0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
(本小题12分)
给出以下一个算法 的程序(如图所示),
的程序(如图所示),
(1)该程序的功能是;
(2)请用直到型循环结构画出相应算法的程序框图.
(本小题10分)
已知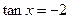 ,求下列各式的值
,求下列各式的值
(1)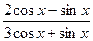 (2)
(2)
(Ⅰ)在复数范围内解方程 (i为虚数单位)
(i为虚数单位)
(Ⅱ)设z是虚数,ω=z+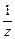 是实数,且-1<ω<2
是实数,且-1<ω<2
(1)求|z|的值及z的实部的取值范围;
(2)设u=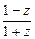 ,求证:u为纯虚数;
,求证:u为纯虚数;
(3)求ω-u2的最小值,