已知 是公差不为零的等差数列,
是公差不为零的等差数列,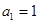 ,且
,且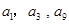 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
已知函数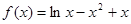 .
.
(Ⅰ)求函数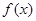 的单调区间;
的单调区间;
(Ⅱ)若关于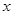 的不等式
的不等式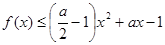 恒成立,求整数
恒成立,求整数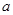 的最小值;
的最小值;
(Ⅲ)若正实数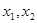 满足
满足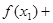
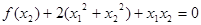 ,证明
,证明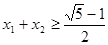 .
.
已知数列 各项均为正数,其前
各项均为正数,其前 项和为
项和为 ,且满足
,且满足 .
.
(1)求 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
某车间小组共12人,需配置两种型号的机器,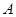 型机器需2人操作,每天耗电
型机器需2人操作,每天耗电 ,能生产出价值4万元的产品;
,能生产出价值4万元的产品; 型机器需3人操作,每天耗电
型机器需3人操作,每天耗电 ,能生产出价值3万元的产品现每天供应车间的电能不多于
,能生产出价值3万元的产品现每天供应车间的电能不多于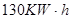 ,问该车间小组应如何配置两种型号的机器,才能使每天的产值最大?最大值是多少?
,问该车间小组应如何配置两种型号的机器,才能使每天的产值最大?最大值是多少?
已知不等式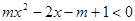
(1)若对于所有的实数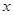 不等式恒成立,求
不等式恒成立,求 的取值范围;
的取值范围;
(2)设不等式对于满足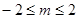 的一切
的一切 的值都成立,求
的值都成立,求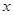 的取值范围.
的取值范围.
已知向量 ,
, .令
.令 ,
,
(1)求 的最小正周期;
的最小正周期;
(2)当 时,求
时,求 的最小值以及取得最小值时
的最小值以及取得最小值时 的值.
的值.