某车间小组共12人,需配置两种型号的机器,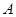 型机器需2人操作,每天耗电
型机器需2人操作,每天耗电 ,能生产出价值4万元的产品;
,能生产出价值4万元的产品; 型机器需3人操作,每天耗电
型机器需3人操作,每天耗电 ,能生产出价值3万元的产品现每天供应车间的电能不多于
,能生产出价值3万元的产品现每天供应车间的电能不多于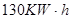 ,问该车间小组应如何配置两种型号的机器,才能使每天的产值最大?最大值是多少?
,问该车间小组应如何配置两种型号的机器,才能使每天的产值最大?最大值是多少?
选修4—1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.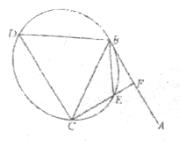
(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,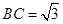 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
已知函数 ,其中
,其中 .
.
(1)当a=3,b=-1时,求函数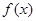 的最小值;
的最小值;
(2)当a>0,且a为常数时,若函数 对任意的
对任意的 ,总有
,总有 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.
已知椭圆C: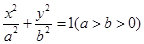 过点
过点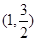 ,且椭圆C的离心率为
,且椭圆C的离心率为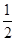 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线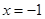 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线 .证明:直线
.证明:直线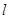 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.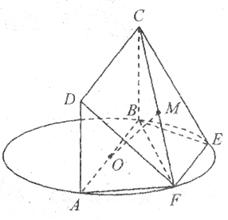
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为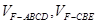 ,求
,求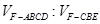 .
.
某高校在2012年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示.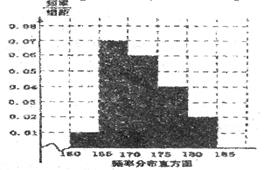
(1)求第三、四、五组的频率;
(2)为了以选拔出最优秀的学生,学校决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名学生进入第二轮面试,求第三、四、五组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第四组至少有一名学生被甲考官面试的概率.