已知函数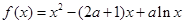 .
.
(1)求函数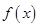 在区间
在区间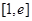 上的最小值;
上的最小值;
(2)设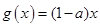 ,其中
,其中 ,判断方程
,判断方程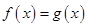 在区间
在区间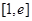 上的解的个数(其中
上的解的个数(其中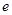 为无理数,约等于
为无理数,约等于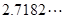 且有
且有 ).
).
已知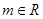 ,函数
,函数
(1)求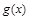 的极小值;
的极小值;
(2)若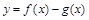 在
在 上为单调增函数,求
上为单调增函数,求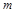 的取值范围;
的取值范围;
(3)设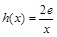 ,若在
,若在 (
(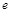 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个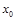 ,使得
,使得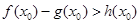 成立,求
成立,求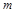 的取值范围.
的取值范围.
设椭圆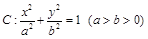 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为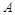 ,离心率为
,离心率为 ,在
,在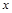 轴负半轴上有一点
轴负半轴上有一点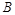 ,且
,且
(1)若过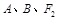 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点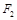 作斜率为
作斜率为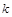 的直线
的直线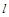 与椭圆C交于
与椭圆C交于 两点,在
两点,在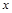 轴上是否存在点
轴上是否存在点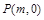 ,使得以
,使得以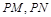 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.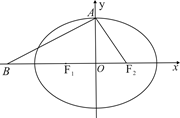
设数列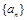 的前
的前 项和为
项和为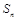 ,且满足
,且满足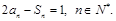
(1)求数列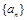 的通项公式;
的通项公式;
(2)在数列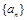 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列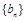 ,在
,在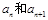 两项之间插入
两项之间插入 个数,使这
个数,使这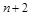 个数构成等差数列,求
个数构成等差数列,求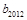 的值;
的值;
(3)对于(2)中的数列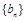 ,若
,若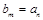 ,并求
,并求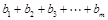 (用
(用 表示).
表示).
如图,在边长为4的菱形 中,
中, .点
.点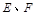 分别在边
分别在边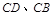 上,点
上,点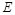 与点
与点 不重合,
不重合,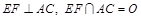 .沿
.沿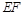 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面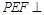 平面
平面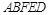 .
.
(1)求证: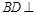 平面
平面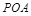 ;
;
(2)设点 满足
满足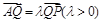 ,试探究:当
,试探究:当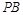 取得最小值时,直线
取得最小值时,直线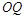 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于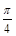 ?并说明理由.
?并说明理由.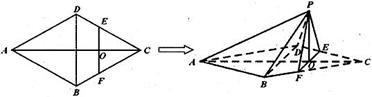
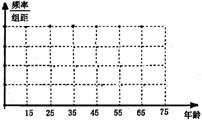
目前南昌市正在进行师大地铁站点围挡建设,为缓解北京西路交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
(1)完成被调查人员年龄的频率分布直方图;
(2)若从年龄在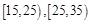 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.