(本小题满分12分)电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选项,但都只有一个选项是正确的。问题A回答正确可得奖金m元,问题B回答正确可得奖金n元。
活动规定:①参与者可任意选择答题顺序;②如果第一个问题回答错误则该参与者猜奖活动中止。
一个参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题,试确定回答问题的顺序,使获奖金额的期望值较大。
已知双曲线 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
(1)求双曲线C的方程;
(2)设 (O为坐标原点),求t的取值范围
(O为坐标原点),求t的取值范围
若 P为椭圆 上任意一点,
上任意一点,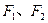 为左、右焦点,
为左、右焦点,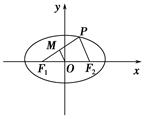
(1)若 的中点为M,求证:
的中点为M,求证: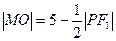 ;
;
(2)若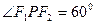 ,求
,求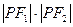 之值;
之值;
(3)椭圆上是否存在点P,使 ,若存在,求出P点的坐标,
,若存在,求出P点的坐标,
若不存在,请说明理由。
如图所示,直三棱柱 ,底面
,底面 中,
中, ,棱
,棱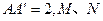 分别是
分别是 的中点.
的中点.
(1)求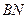 的长;
的长;
(2)求异面直线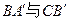 所成角的余弦值.
所成角的余弦值.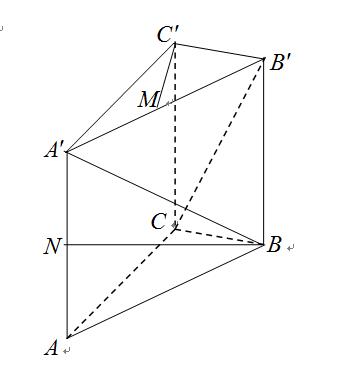
已知命题 :方程
:方程 有两个不等的负实根;命题
有两个不等的负实根;命题 :方程
:方程 无实根,若“p或q”为真命题,“p且q”为假命题,求实数m的取值范围
无实根,若“p或q”为真命题,“p且q”为假命题,求实数m的取值范围
(本小题满分10分)
已知函数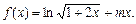
(1)当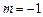 时,求函数
时,求函数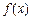 的最大值;
的最大值;
(2)当 时,设点
时,设点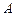 、
、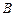 是函数
是函数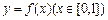 的图象上任意不同的两点,求证:直线
的图象上任意不同的两点,求证:直线 的斜率
的斜率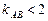 .
.