如图,直线y= 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点 是劣弧AO上一动点(
是劣弧AO上一动点( 点与
点与 不重合).抛物线y=-
不重合).抛物线y=- 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,
(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连 交
交 于点
于点 ,延长
,延长 至
至 ,使
,使 ,试探究当点
,试探究当点 运动到何处时,直线
运动到何处时,直线 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.
如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.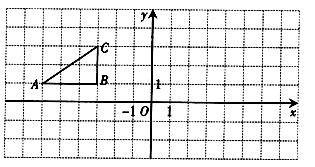
(1)以原点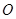 为对称中心,画出与△ABC关于原点
为对称中心,画出与△ABC关于原点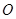 对称的△A1B1C1,A1 的坐标是 .
对称的△A1B1C1,A1 的坐标是 .
(2)将原来的△ABC绕着点B顺时针旋转90°得到△A2B2C2,试在图上画出△A2B2C2的图形.
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.试猜想BD,CE,DE三者的数量关系?(直接写出结果)
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=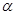 ,其中
,其中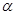 为任意锐角或钝角.请问(1)中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3) 拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.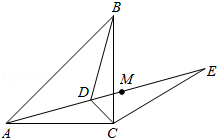
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
如图,在等腰直角△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE.连接DE、DF、EF.
(1)求证:△ADF≌△CEF;
(2)试判断△DFE的形状,并说明理由.
将4个数a b c d排成两行,两列,两边各加一条竖直线记成 ,定义
,定义 =ad﹣bc.上述记号叫做2阶行列式,若
=ad﹣bc.上述记号叫做2阶行列式,若 =
= .求
.求 的值.
的值.