上海理）甲厂以x 千克/小时的速度运输生产某种产品（生产条件要求
），每小时可获得利润是
元.
(1)要使生产该产品2小时获得的利润不低于3000元，求x的取值范围；
(2)要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求最大利润.
（本小题满分12分）
已知集合
, 
.
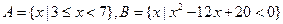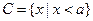（1）求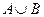
；
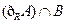
（2）若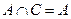
,求
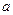的取值范围
（本小题满分14分
函数
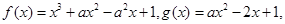实数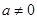
．
（I）若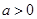
，求函数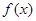
的单调区间；
（II）当函数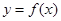
与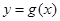
的图象只有一个公共点且
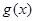存在最小值时，记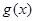的最小值为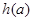
，求的值域；
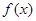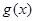（III）若与在区间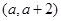
内均为增函数，求
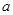的取值范围。
（文）已知函数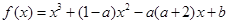
．
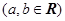（I）若函数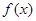的图象过原点，且在原点处的切线斜率是
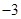，求
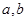的值；
（II）若函数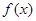在区间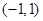
上不单调，求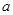的取值范围
（本小题满分12分）
数列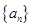
满足
（1）求数列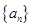的通项公式；
(2)令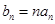
，求数列的前n
项和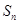
（本小题满分12分）
已知
是等比数列, 
，
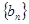是等差数列，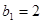
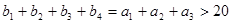
（1）求数列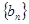的通项公式；
（2）求数列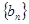的前n项和
；
（3）设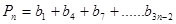
，
其中n=1,2,......,试比较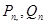
的大小。
（本小题满分12分）
在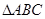
中，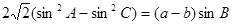
,外接圆半径为
。
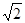（1）求角C;
（2）求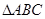面积的最大值