如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,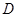 是AC的中点,已知
是AC的中点,已知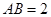 ,
, .
.
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥 的体积.
的体积.
若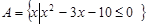 ,
,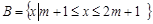
(1)当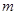 =1时,求
=1时,求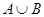
(2)若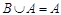 ,求
,求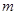 的取值范围.
的取值范围.
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.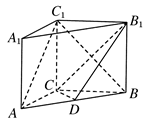
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求: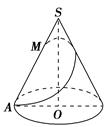
(1)设f(x)为绳子最短长度的平方,求f(x)表达式;
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
如图,△ABC中,AC=BC= AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;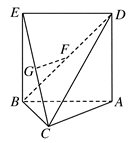
圆柱的高是8 cm,表面积是130 π cm2,求它的底面圆半径和体积.