甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
若数列 满足
满足 ,其中
,其中 为常数,则称数列
为常数,则称数列 为等方差数列,已知等方差数列
为等方差数列,已知等方差数列 满足
满足 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和;
项和;
(3)记 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的 恒成立?请说明理由。
恒成立?请说明理由。
甲、乙两物体分别从相距70m处的两处同时相向运动,甲第一分钟走2m,以后每分钟比前一分钟多走1m,乙每分钟走5m。
(1)甲、乙开始运动后几分钟相遇?
(2)如果甲、乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1m,乙继续每分钟走5m,那么开始运动几分钟后第二次相遇?
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C ,其中
,其中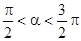 ,
,
(1)若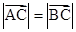 ,求角
,求角 的值;
的值;
(2)若 ,求
,求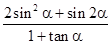 的值。
的值。
等差数列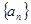 中,前三项分别为
中,前三项分别为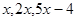 ,前
,前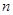 项和为
项和为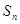 ,且
,且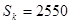 。
。
(1)、求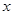 和
和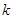 的值;(2)、求T=
的值;(2)、求T=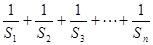
已知 中,
中, 求:(1)边b的长;(2)求
求:(1)边b的长;(2)求 的面积。
的面积。