某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次停止摸奖的概率；
（2）记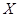
为1名顾客摸奖获得的奖金数额，求随机变量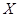的分布律和数学期望．
（本小题满分12分）如图，矩形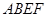
所在的平面与等边
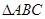所在的平面垂直，
，
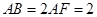为
的中点．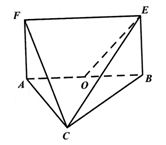
（1）求证：
；
（2）求二面角
的余弦值．
（本小题满分12分）已知数列
满足：
,
，
，（
）．
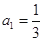（1）求证：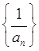
是等差数列，并求出
；
（2）证明：
．
如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=600，PA=AC=a，PB=PD=
，点E在PD上，且PE：ED=2：1．
（Ⅰ）证明PA⊥平面ABCD；
（Ⅱ）求以AC为棱，EAC与DAC为面的二面角
的大小；
（Ⅲ）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论．
如图，在圆锥
中，已知PO=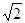
，圆O的直径AB=2，C是弧AB的中点，D为AC的中点．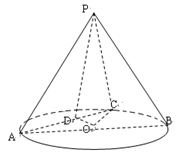
（1）求异面直线PD和BC所成的角的正切值；
（2）求直线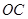
和平面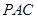
所成角的正弦值．
如图，在正方体ABCD－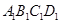
中，棱长为a，E为棱CC1上的的动点．
（1）求证：A1E⊥BD；
（2）当E恰为棱CC1的中点时，求证：平面A1BD⊥平面EBD．