求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
已知sina=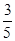 ,aÎ(
,aÎ(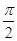 ,p),cosb=-
,p),cosb=-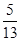 ,b是第三象限的角.
,b是第三象限的角.
⑴ 求cos(a-b)的值;
⑵ 求sin(a+b)的值;
⑶ 求tan2a的值.
在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,
求⑴ ∠ADB的大小;⑵ BD的长.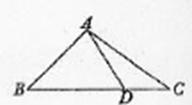
已知函数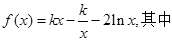
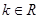 ;
;
(1)若函数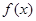 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数 的取值范围。
的取值范围。
(2)若函数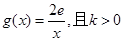 ,若在[1,e]上至少存在一个x的值使
,若在[1,e]上至少存在一个x的值使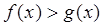 成立,求实数
成立,求实数 的取值范围。
的取值范围。
已知函数 ,
,
(1)求函数 的定义域;
的定义域;
(2)求函数 在区间
在区间 上的最小值;
上的最小值;
(3)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 的定义域上的任意
的定义域上的任意 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.