为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量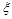 ,求
,求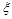 的分布列和数学期望E
的分布列和数学期望E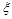
如图,四棱锥 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, ,
, ,
, 面
面 ,设
,设 为
为 中点,点
中点,点 在线段
在线段 上且
上且 .
.
(1)求证: 平面
平面 ;
;
(2)设二面角 的大小为
的大小为 ,若
,若 ,求
,求 的长.
的长.
设数列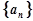 的前n项和为
的前n项和为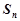 ,
,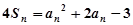 ,且
,且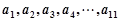 成等比数列,当
成等比数列,当 时,
时,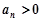 .
.
(1)求证:当 时,
时, 成等差数列;
成等差数列;
(2)求 的前n项和
的前n项和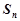 .
.
已知函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
已知函数 ,
, ,
, .
.
(1)若当 时,恒有
时,恒有 ,求
,求 的最大值;
的最大值;
(2)若当 时,恒有
时,恒有 ,求
,求 的取值范围.
的取值范围.
已知直线 的参数方程为
的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(1)把圆C的极坐标方程化为直角坐标方程;
(2)将直线 向右平移h个单位,所得直线
向右平移h个单位,所得直线 与圆C相切,求h.
与圆C相切,求h.