为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求 和
和 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: )
)
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的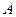 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以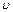 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过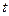 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(本小题满分12分)
曲线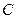 是以原点为中心,以抛物线
是以原点为中心,以抛物线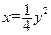 的焦点F为右焦点,离心率为
的焦点F为右焦点,离心率为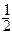 的椭圆,且过F的直线交椭圆C于P、Q两点,M是
的椭圆,且过F的直线交椭圆C于P、Q两点,M是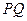 中点.
中点.
(1)求椭圆C的方程;
(2)当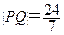 时,求直线PQ的方程.
时,求直线PQ的方程.
(本小题满分12分)
已知数列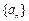 的前n项和
的前n项和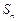 满足:
满足: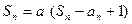 (
(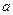 为常数,
为常数,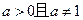 ).
).
(Ⅰ)求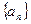 的通项公式;
的通项公式;
(Ⅱ)设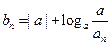 ,若数列
,若数列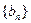 的前n项和
的前n项和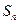 中,
中,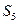 为最大值,求
为最大值,求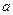 的取值范围.
的取值范围.
(本小题满分12分)
在平面直角坐标系中,点M的坐标为(x,y),点P的坐标为(2,3).
(I)在一个密封的盒子中,放有标号为1,2,3 ,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“
,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“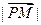 =
=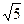 ”的概率;
”的概率;
(II)若利用计算机随机在[0,4]上先后取两个数分别记为x,y,求点M满足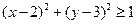 的概率
的概率
(本小题满分12分)
如图,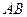 为圆
为圆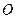 的直径,点
的直径,点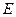 、
、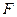 在圆
在圆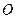 上,
上,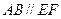 ,矩形
,矩形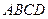 所在平面和圆
所在平面和圆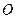 所在的平面互相垂直.
所在的平面互相垂直.
(Ⅰ)求证:AD∥平面BCF;
(Ⅱ)求证:平面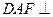 平面
平面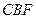 ;
;