从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
 |
 |
 |
 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在 的频率;
的频率;
(2)用分层抽样的方法从重量在 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在 和
和 中各有1个的概率.
中各有1个的概率.
设
分别是椭圆
的左右焦点,
是
上一点且
与
轴垂直,直线
与
的另一个交点为
.
(1)若直线
的斜率为
,求
的离心率;
(2)若直线
在
轴上的截距为
,且
,求
.
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评优.
如图,四棱锥
中,底面
为矩形,
平面
,
是
的中点.
(1)证明:
//平面
;
(2)设
,三棱锥
的体积
,求
到平面
的距离.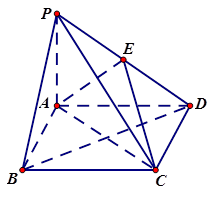
四边形
的内角
与
互补,
.
(1)求
和
;
(2)求四边形
的面积.
设函数
,记
的解集为
,
的解集为
.
(1)求
;
(2)当
时,证明:
.