随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: ,2;
,2; ,7;
,7; ,10;
,10; ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为 ,求
,求 的数学期望.
的数学期望.
(必做题)在正方体 中,如图E、F分别是
中,如图E、F分别是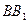 ,CD的中点,
,CD的中点,
(1)求证: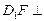 平面ADE;(2)cos
平面ADE;(2)cos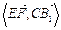 .
.
(本题满分16分)已知圆O: 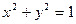 ,圆C:
,圆C: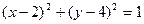 ,由两圆外一点
,由两圆外一点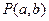 引两圆切线PA、PB,切点分别为A、B,满足|PA|="|PB|." (1)求实数a、b间满足的等量关系;(2)求切线长|PA|的最小值;(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
引两圆切线PA、PB,切点分别为A、B,满足|PA|="|PB|." (1)求实数a、b间满足的等量关系;(2)求切线长|PA|的最小值;(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.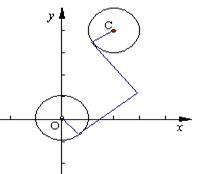
(本题满分13分)已知函数: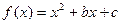 ,其中:
,其中: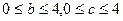 ,且
,且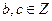 ,记函数
,记函数 满足条件:
满足条件: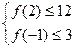 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。
已知函数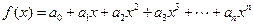 (n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(2)当n为奇函数时,设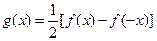 ,是否存在自然数m和M,使不等式m<
,是否存在自然数m和M,使不等式m<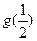 <M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
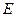 、
、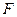 是椭圆
是椭圆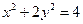 的左、右焦点,
的左、右焦点,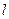 是椭圆的右准线,点
是椭圆的右准线,点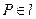 ,过点
,过点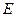 的直线交椭圆于
的直线交椭圆于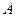 、
、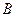 两点.(1)当
两点.(1)当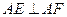 时,求
时,求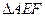 的面积;(2)当
的面积;(2)当 时,求
时,求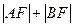 的大小;(3)求
的大小;(3)求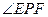 的最大值.
的最大值.