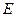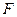、
是椭圆
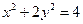的左、右焦点，
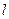是椭圆的右准线，点
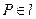，过点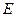的直线交椭圆于
、
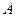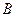两点.（1）当
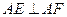时，求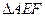
的面积；（2）当
时，求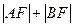
的大小；（3）求
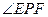的最大值.
（本小题满分13分）
已知函数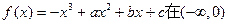
上是减函数，在
（0，1）上是增函数，函数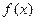
在R上有三个零点，且1是其中一个零点。
（1）求b的值；
（2）求
的取值范围。
（本小题满分12分）
已知函数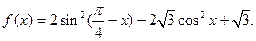
（1）求
的最小正周期和单调递减区间；
（2）求
上恒成立，求实数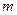
的取值范围。
（本小题满分12分）
函数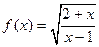
的定义域为集合A，关于x的不等式
的解集为B，求使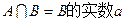
的取值范围。
（本小题满分10分）选修4
—5：不等式选讲
设函数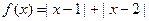
（Ⅰ）画出函数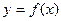
的图像；
（Ⅱ）若不等式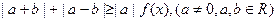
恒成立，求实数
的范围。
（本小题满分10分）选修4一l：几何证明选讲
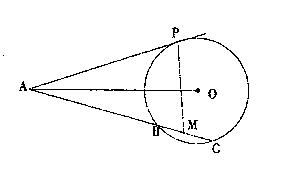
如图，已知AP是圆O的切线，P为切点，AC是圆O的割线，与圆O交于B，C两点，圆心O在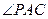
的内部，点M是BC的中点．
（Ⅰ）证明A，P，0，M四点共圆；
（Ⅱ）求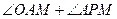
的大小。