如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=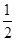 CD.
CD.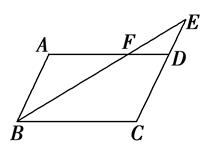
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求▱ABCD的面积.
已知P={x|a-4<x<a+4},Q={x|x2-4x+3<0},若x∈P是x∈Q的必要条件,求实数a的取值范围.
下列命题中,判断条件p是条件q的什么条件:
(1)p:|x|=|y|,q:x=y.
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形.
已知 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2) 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有 .
.
写出下列命题的逆命题、否命题、逆否命题,并指出他们的真假:
(1)若xy=0,则x,y中至少有一个是0;
(2)若x>0,y>0,则xy>0;
把命题“未位数是0的整数可以被5整除”改写为“若p则q”的形式,并写出它的逆命题、否命题与逆否命题