在如下图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ =370的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行。劲度系数K=5N/m的轻弹簧一端固定在0点,一端用另一轻绳穿过固定的光滑小环D与A相连,弹簧处于原长,轻绳恰好拉直,DM垂直于斜面。水平面处于场强E=5×104N/C、方向水平向右的匀强电场中。已知A、B的质量分别为mA ="0." 1kg和mB ="0." 2kg,B所带电荷量q="+4" xl0-6C。设两物体均视为质点,不计滑轮质量和摩擦,绳不可伸长,弹簧始终在弹性限度内,B电量不变。取g= l0m/s2,sin370 =0.6,cos370 =0.8。
(1)求B所受静摩擦力的大小;
(2)现对A施加沿斜面向下的拉力F,使A以加速度a="0." 6m/s2开始做匀加速直线运动。A从M到N的过程中,B的电势能增加了△Ep=0.06J。已知DN沿竖直方向,B与水平面间的动摩擦因数μ=0.4。求A到达N点时拉力F的瞬时功率。
 一辆汽车,以36km/h的速度匀速行驶10s,然后以1m/s2的加速度匀加速行驶10s,求:
一辆汽车,以36km/h的速度匀速行驶10s,然后以1m/s2的加速度匀加速行驶10s,求:
(1)汽车在这20s内的位移是多大?
(2)汽车在加速的10s内的平均速度是多大?
如图所示,光滑导轨与水平面成θ角,导轨宽L。匀强磁场磁感应强度为B。金属杆长也为L,质量为m,水平放在导轨上。当回路总电流为I1时,金属杆正好能静止。求:
(1)B至少多大?这时B的方向如何?
(2)若保持B的大小不变而将B的方向改为竖直向上,
应把回路总电流I2调到多大才能使金属杆保持静止?
一宇宙人在太空(万有引力可以忽略不计)玩垒球。如图所示,辽阔的太空球场半侧为匀强电场,另半 侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场
侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场 方向与界面垂直,磁场方向垂直纸面向里,电场强度大小
方向与界面垂直,磁场方向垂直纸面向里,电场强度大小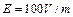 。宇宙人位于电场一侧距界面为
。宇宙人位于电场一侧距界面为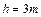 的
的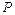 点,
点,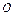 为
为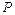 点至界面垂线的垂
点至界面垂线的垂 足,
足,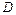 点位于纸面上
点位于纸面上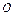 点的右侧,
点的右侧,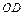 与磁场的方向垂直。垒球的质量
与磁场的方向垂直。垒球的质量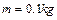 ,电量
,电量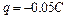 。宇宙人从
。宇宙人从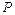 点以初速度
点以初速度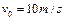 平行于界面投出垒球,要使垒球第一次通过界面时就击中
平行于界面投出垒球,要使垒球第一次通过界面时就击中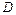 点,求:(计算结果保留三位有效数字)
点,求:(计算结果保留三位有效数字)
(1)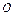 、
、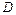 两点之间的距离。
两点之间的距离。
(2)垒球从抛出到第一次回到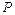 点的时间。
点的时间。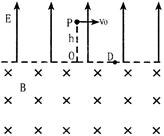
在图甲中,电源的电动势E=9.0V,电源内电阻可忽略不计;G为小量程的电 流表,电流表内阻Rg保持不变,R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示。闭合开关S,当R的温度等于20oC时,电流表示数I1=2mA,则当电流表的示数I2=3.6mA时,热敏电阻R的温度为多少?
流表,电流表内阻Rg保持不变,R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示。闭合开关S,当R的温度等于20oC时,电流表示数I1=2mA,则当电流表的示数I2=3.6mA时,热敏电阻R的温度为多少?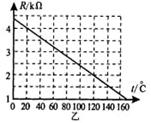

用电阻为18 Ω的均匀导线弯成如图中直径D ="0.80" m的封闭金属圆环,环上AB弧所对应的圆心角为60º,将圆环垂直于磁感线方向固定在磁感应强度B ="0.50" T的匀强磁场中,磁场方向垂直于纸面向里.一根每米电阻为1.25 Ω的直导线PQ,沿圆环平面向左以3.0 m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
(1)直导线AB段产生的感应电动势,并指明该段直导线中电流的方向.
(2)此时圆环上发热损耗的电功率.