1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于真空中的两个D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直. 设两D形盒之间所加的交流电压为U,被加速的粒子质量为m、电量为q,粒子从D形盒一侧开始被加速(初动能可以忽略),经若干次加速后粒子从D形盒边缘射出.

求:(1)粒子从静止开始第1次经过两D形盒间狭缝加速后的速度大小
(2)粒子第一次进入D型盒磁场中做圆周运动的轨道半径
(3)粒子至少经过多少次加速才能从回旋加速器D形盒射出
某同学利用DIS实验系统研究一定质量理想气体的状态变化,实验后计算机屏幕显示如图所示的P-V图象.已知在状态A时气体的体积为TA=127°,问:
①气体在状态B和状态C的温度是多少?
②从状态B到状态C这个过程中,会经过一个与状态A温度相同的状态D,则状态D的压强是多少?
③从状态A经状态B到状态C这个过程中,气体对外做功多少?
如图所示,x轴为水平方向,y轴为竖直方向,在第一、三、四象限内有垂直纸面向里的匀强磁场B(图中没画),在x轴上方的与X轴夹角为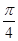 的匀强电强E1,在x轴下方有与竖起直向上的匀强电场E2。一个质量为m、电荷量为q的带正电的小球在第一象限的P(x0,,y0)点,以速度v0竖直向下匀速运动(在第一象限内),当带电小球从第一象限进入第四象限后,第一象限内的磁场消失,小球最终又回到P点。已知:
的匀强电强E1,在x轴下方有与竖起直向上的匀强电场E2。一个质量为m、电荷量为q的带正电的小球在第一象限的P(x0,,y0)点,以速度v0竖直向下匀速运动(在第一象限内),当带电小球从第一象限进入第四象限后,第一象限内的磁场消失,小球最终又回到P点。已知: ,
, ,重力加速度g。求:
,重力加速度g。求: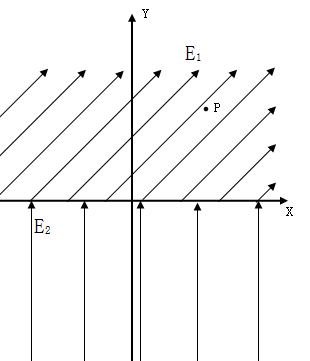
(1)磁感应强度B和电场强度E1;
(2)带电小球的从P点出发到重新回到P点的运动时间和P点的纵坐标y0;
(3)带电小球的从P点出发到重新回到P点的整个过程中电场力做的功和在这个过程中重力做功的最大值。
如图所示,A、B两点在同一水平线上,B点在斜面的延长线上,斜面倾角θ=45°。甲物体在A点以10m/s初速度水平抛出,恰好落在斜面项端,并刚好沿斜面下滑,经过时间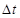 后,乙物体在B点以20m/s初速度水平抛出,正好在斜面上某点到与甲物体相碰。已知:甲物体与斜面的动摩擦因数是
后,乙物体在B点以20m/s初速度水平抛出,正好在斜面上某点到与甲物体相碰。已知:甲物体与斜面的动摩擦因数是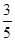 。求:
。求:
(1)A、B两点间的距离;
(2)乙物体比甲物体后抛的时间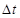 。
。
底面光滑的木板B和C长度均为L,小木块A静止于B的右端,C以初速度 水平向右匀速直线运动与B发生正碰并且碰后粘在一起, B、C质量相等均为m,A的质量为
水平向右匀速直线运动与B发生正碰并且碰后粘在一起, B、C质量相等均为m,A的质量为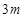 。重力加速度取
。重力加速度取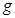 。
。
(1)求木板B的最大速度;
(2)若要求物块A不会掉在水平面上,则物块与木板间的动摩擦因数μ至少是多大。
一束平行光照射到半球形玻璃砖上,该束光线的边界分别为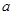 和
和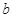 。已知玻璃砖半径为
。已知玻璃砖半径为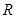 ,折射率为
,折射率为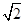 ,如下图所示,下边界
,如下图所示,下边界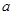 处光线恰好沿半径方向,在O点恰好产生全反射。求:
处光线恰好沿半径方向,在O点恰好产生全反射。求: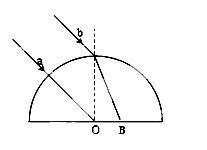
(1)玻璃砖发生全反射的临界角;
(2)光束ab在玻璃砖底产生的两个光斑的距离OB。