如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球。现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=1.0m,A、B两点的高度差h=0.5m,重力加速度g取10m/s2,不计空气阻力影响,求: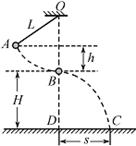
⑴地面上DC两点间的距离s;⑵轻绳所受的最大拉力大小。
如图所示,将一个绝热的汽缸竖直放置在水平桌面上,在汽缸内用一个活塞封闭了一定质量的气体。在活塞上面放置一个物体,活塞和物体的总质量为10kg,活塞的横截面积为: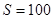 cm2。已知外界的大气压强为
cm2。已知外界的大气压强为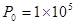 Pa,不计活塞和汽缸之间的摩擦力。在汽缸内部有一个电阻丝,电阻丝的电阻值
Pa,不计活塞和汽缸之间的摩擦力。在汽缸内部有一个电阻丝,电阻丝的电阻值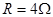 ,电源的电压为12V。接通电源10s后活塞缓慢升高
,电源的电压为12V。接通电源10s后活塞缓慢升高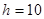 cm,求这一过程中气体的内能变化量。若缸内气体的初始温度为27℃,体积为
cm,求这一过程中气体的内能变化量。若缸内气体的初始温度为27℃,体积为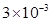 m3,试求接通电源10s后缸内气体的温度是多少?
m3,试求接通电源10s后缸内气体的温度是多少?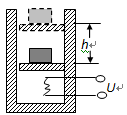
如图所示,在坐标原点O处,能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子。在O点右侧有一半径为R的圆形薄板,薄板中心O′位于x轴上,且与x轴垂直放置,薄板的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电量为q,速率为v,重力不计。
(1)要使y轴右侧所有运动的粒子都能打到薄板MN上,可在y轴右侧加一平行于x轴的匀强电场,则场强的最小值E0为多大?在电场强度为E0时,打到板上的粒子动能为多大?
(2)要使薄板右侧的MN连线上都有粒子打到,可在整个空间加一方向垂直纸面向里的匀强磁场,则磁场的磁感应强度不能超过多少(用m、v、q、R表示)?若满足此条件,从O点发射出的所有带电粒子中有几分之几能打在板的左边?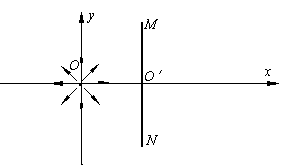
如图所示,一个可视为质点的物块,质量为m=2 kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为u=3 m/s。已知圆弧轨道半径R=0.8 m,皮带轮的半径r=0.2m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=6m,重力加速度g=10m/s2。求: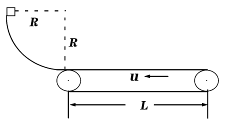
(1)皮带轮转动的角速度多大?
(2)物块滑到圆弧轨道底端时对轨道的作用力;
(3)物块将从传送带的哪一端离开传送带?物块在传送带上克服摩擦力所做的功为多大?
当物体从高空下落时,所受阻力会随物体的速度增大而增大,因此经过下落一段距离后将匀速下落,这个速度称为此物体下落的收尾速度。研究发现,在相同环境条件下,球形物体的收尾速度仅与球的半径和质量有关.下表是某次研究的实验数据
| 小球编号 |
A |
B |
C |
D |
E |
| 小球的半径(×10-3m) |
0.5 |
0.5 |
1.5 |
2 |
2.5 |
| 小球的质量(×l0-6kg) |
2 |
5 |
45 |
40 |
100 |
| 小球的收尾速度(m/s) |
16 |
40 |
40 |
20 |
32 |
(1)根据表中的数据,求出B球与C球在达到终极速度时所受阻力之比。
(2)根据表中的数据,归纳出球型物体所受阻力f与球的速度大小及球的半径的关系(写出有关表达式、并求出比例系数)。
质量m=1.5kg的物块(可视为质点)在水平恒力F作用下,从水平面上A点由静止开始运动,运动一段距离撒去该力。物块继续滑行t=2.0s停在B点,已知A、B两点间的距离s=5.0m,物块与水平面间的动摩擦因数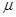 =0.20,求恒力F多大.(g=10m/s2)
=0.20,求恒力F多大.(g=10m/s2)