为了寻找马航 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
, 海里,且
海里,且
 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口 正东
正东 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛 装上补给物资供给科考船.该船沿
装上补给物资供给科考船.该船沿 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线 围成的三角形
围成的三角形 的面积
的面积 最小时,这种补给方案最优.
最小时,这种补给方案最优.
(1)求 关于
关于 的函数关系式
的函数关系式 ;
;
(2)应征调位于港口正东多少海里处的补给船只,补给方案最优?
数列 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列。
的等比数列。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的通项公式。
的通项公式。
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分
(1)(本小题满分7分)选修4-2:矩阵与变换
变换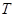 是将平面上每个点
是将平面上每个点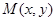 的横坐标乘
的横坐标乘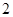 ,纵坐标乘
,纵坐标乘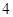 ,变到点
,变到点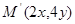 .
.
(Ⅰ)求变换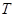 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换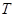 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线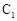 的极坐标方程为:
的极坐标方程为: ,直线
,直线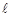 的参数方程为:
的参数方程为: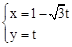 (
(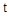 为参数).
为参数).
(Ⅰ)求曲线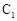 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线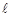 上有一定点
上有一定点 ,曲线
,曲线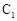 与
与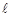 交于M,N两点,求
交于M,N两点,求 的值.
的值.
(3)(本小题满分7分)选修4-5:不等式选讲
已知 为实数,且
为实数,且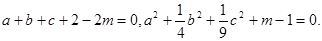
(Ⅰ)求证: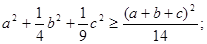
(Ⅱ)求实数m的取值范围.
定义函数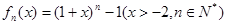 其导函数记为
其导函数记为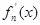 .
.
(Ⅰ)求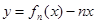 的单调递增区间;
的单调递增区间;
(Ⅱ)若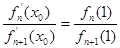 ,求证:
,求证: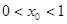 ;
;
(Ⅲ)设函数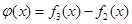 ,数列
,数列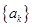 前
前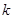 项和为
项和为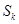 ,
,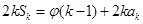 ,其中
,其中 .对于给定的正整数
.对于给定的正整数 ,数列
,数列 满足
满足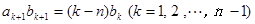 ,且
,且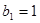 ,求
,求 .
.
已知椭圆 的离心率为
的离心率为 ,直线
,直线 过点
过点 ,
, ,且与椭圆
,且与椭圆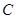 相切于点
相切于点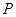 .
.
(Ⅰ)求椭圆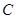 的方程;
的方程;
(Ⅱ)过点 的动直线与曲线
的动直线与曲线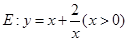 相交于不同的两点
相交于不同的两点 、
、 ,曲线
,曲线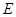 在点
在点 、
、 处的切线交于点
处的切线交于点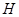 .试问:点
.试问:点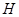 是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.
是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.
有甲、乙等7名选手参加一次演讲比赛,采用抽签的方式随机确定每名选手的演出顺序(序号为1,2,…,7).
(Ⅰ)甲选手的演出序号是1的概率;
(Ⅱ)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(Ⅲ)设在甲、乙两名选手之间的演讲选手个数为 ,求
,求 的分布列与期望.
的分布列与期望.