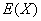本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分
(1)(本小题满分7分)选修4-2:矩阵与变换
变换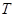 是将平面上每个点
是将平面上每个点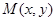 的横坐标乘
的横坐标乘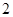 ,纵坐标乘
,纵坐标乘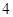 ,变到点
,变到点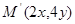 .
.
(Ⅰ)求变换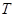 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换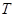 的作用下变成了什么图形?
的作用下变成了什么图形?
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线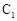 的极坐标方程为:
的极坐标方程为: ,直线
,直线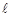 的参数方程为:
的参数方程为: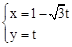 (
(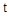 为参数).
为参数).
(Ⅰ)求曲线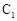 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线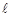 上有一定点
上有一定点 ,曲线
,曲线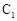 与
与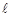 交于M,N两点,求
交于M,N两点,求 的值.
的值.
(3)(本小题满分7分)选修4-5:不等式选讲
已知 为实数,且
为实数,且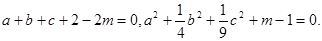
(Ⅰ)求证: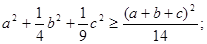
(Ⅱ)求实数m的取值范围.
已知向量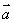 =(
=(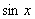 ,1),
,1), =(
=( ,1),
,1),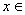 R.
R.
(1)当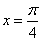 时,求向量
时,求向量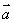 +
+ 的坐标;
的坐标;
(2)若函数 |
|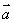 +
+ |2
|2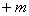 为奇函数,求实数
为奇函数,求实数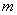 的值.
的值.
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D= .
.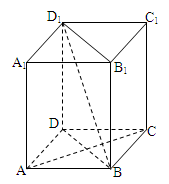
(1)求直线D1B与平面ABCD所成角的大小;
(2)求证:AC⊥平面BB1D1D.
一批食品,每袋的标准重量是50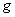 ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:
,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位: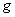 ),并得到其茎叶图(如图).
),并得到其茎叶图(如图).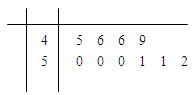
(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;
(2)若某袋食品的实际重量小于或等于47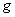 ,则视为不合格产品,试估计这批食品重量的合格率.
,则视为不合格产品,试估计这批食品重量的合格率.
已知函数 (
(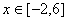 )的图象如图.根据图象写出:
)的图象如图.根据图象写出: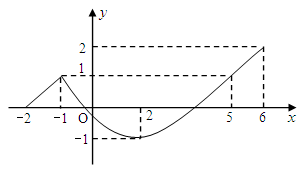
(1)函数 的最大值;
的最大值;
(2)使 的
的 值.
值.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望