已知曲线 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,设点
,设点 (
( ).
).
(1)指出 ,并求
,并求 与
与 的关系式(
的关系式( );
);
(2)求 (
( )的通项公式,并指出点列
)的通项公式,并指出点列 ,
, ,
, ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由;
(3)令 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
已知数列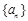 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列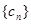 的前n项和Sn.
的前n项和Sn.
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;
(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分 的概率分布列及数学期望。
的概率分布列及数学期望。
△ABC中,a,b,c分别是角A,B,C的对边, ,且
,且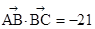 ,
,
(Ⅰ)求△ABC的面积;(Ⅱ)若a=7,求角∠C
已知函数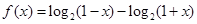 ,
,
(1)求函数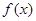 的定义域;
的定义域;
(2)判断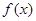 的奇偶性;
的奇偶性;
(3)方程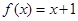 是否有根?如果有根
是否有根?如果有根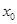 ,请求出一个长度为
,请求出一个长度为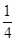 的区间
的区间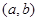 ,使
,使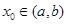 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间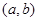 的长度
的长度 ).
).
已知两直线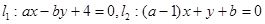 ,求分别满足下列条件的
,求分别满足下列条件的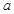 、
、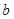 的值.
的值.
(1)直线 过点
过点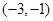 ,并且直线
,并且直线 与直线
与直线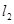 垂直;
垂直;
(2)直线 与直线
与直线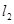 平行,并且坐标原点到
平行,并且坐标原点到 、
、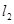 的距离相等.
的距离相等.