如图,直三棱柱 中,
中, ,
,  ,
, 是
是 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点, 为
为 上一点.
上一点.
(1)若 ∥平面
∥平面 ,求
,求 ;
;
(2)平面 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
(本小题满分10分)
在△ABC中,  是方程
是方程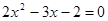 的一个根,
的一个根,
(1)求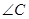 ;
;
(2)当 时,求△ABC周长的最小值.
时,求△ABC周长的最小值.
(本小题满分14分)
已知 是椭圆
是椭圆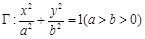 的左右焦点,椭圆
的左右焦点,椭圆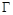 的离心率
的离心率 ,
, 是
是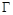 上异于左右顶点的任意一点,且
上异于左右顶点的任意一点,且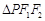 的面积的最大值为1.
的面积的最大值为1.
(Ⅰ)求椭圆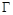 的方程;
的方程;
(Ⅱ)直线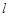 是椭圆在点P处的切线,过
是椭圆在点P处的切线,过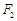 作
作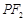 的垂线,交直线
的垂线,交直线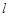 相交于Q,求证:点Q落在一条定直线
相交于Q,求证:点Q落在一条定直线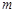 上,并求直线
上,并求直线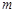 的方程.
的方程.
(本小题满分14分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.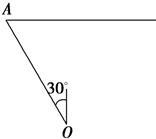
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
(本小题满分12分)
已知 ,设不等式组
,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内整点的个数为
内整点的个数为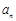 (横、纵坐标均为整数的点称为整点).
(横、纵坐标均为整数的点称为整点).
(Ⅰ)通过研究 的值的规律,求
的值的规律,求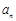 的通项公式;
的通项公式;
(Ⅱ)求证: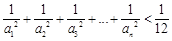 .
.
(本小题满分12分)
已知实数 ,设函数
,设函数 .
.
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若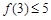 ,求a的取值范围.
,求a的取值范围.