如图,已知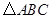 中,
中,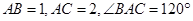 ,点
,点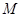 是边
是边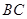 上的动点,动点
上的动点,动点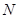 满足
满足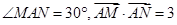 (点
(点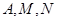 按逆时针方向排列).
按逆时针方向排列).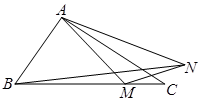
(1)若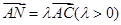 ,求
,求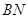 的长;
的长;
(2)求△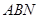 面积的最大值.
面积的最大值.
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?
(本小题满分12分)
如图,平面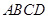 ⊥平面
⊥平面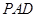 ,
,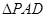 是直角三角形,
是直角三角形, ,四边形
,四边形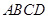 是直角梯形,其中
是直角梯形,其中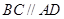 ,
, ,
, ,且
,且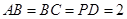 ,
,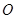 是
是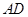 的中点,
的中点,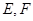 分别是
分别是 的中点.
的中点. 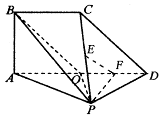
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角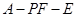 的正切值.
的正切值.
已知数列 是递增数列,且满足
是递增数列,且满足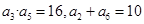 。
。
(1)若 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(2)对于(1)中 ,令
,令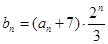 ,求数列
,求数列 的前
的前 项和
项和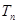 。
。
(本小题满分14分)已知函数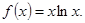
(1)求函数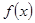 的极值点;
的极值点;
(2)若直线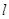 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线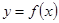 相切,求直线
相切,求直线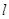 的方程;
的方程;
(3)设函数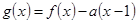 ,其中
,其中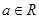 ,求函数
,求函数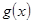 在
在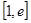 上的最小值.(其中e为自然对数的底数
上的最小值.(其中e为自然对数的底数
(本小题满分12分) 已知椭圆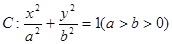 的焦距为
的焦距为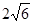 ,椭圆
,椭圆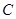 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆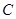 的方程;
的方程;
(Ⅱ)设直线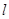
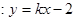 与椭圆
与椭圆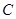 交于
交于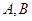 两点,点
两点,点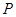 (0,1),且
(0,1),且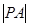 =
=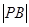 ,求直线
,求直线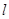 的方程.
的方程.