甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于 分的次数为
分的次数为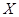 ,求
,求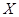 的分布列和数学期望
的分布列和数学期望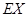 ..
..
(
在区间[0,1]上给定曲线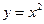 ,
, 轴.
轴.
(1)当面积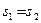 时,求P点的坐标。
时,求P点的坐标。
(2)试在此区间确定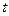 的值,使
的值,使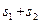 的值最小,并求出最小值。
的值最小,并求出最小值。
已知向量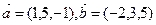 .
.
(1)若
(2)若
(1)当实数 取何值时,复数
取何值时,复数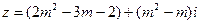 在复平面内对应的点
在复平面内对应的点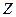 在直线
在直线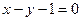 上?
上?
(2)已知 ,如果
,如果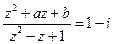 ,求实数
,求实数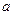 和
和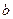 的值。
的值。
(本小题满分14分)
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求f(x)的解析式;
(2)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(3)若当x=1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.
(本小题满分13分)
已知双曲线C: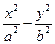 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为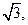 焦点到渐近线的距离为
焦点到渐近线的距离为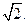
(1)求双曲线C的方程;
(2)已知直线x-y+m =0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
=0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
线y2="4" x上,求m的值.