一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设 为取得红球的个数.
为取得红球的个数.
(1)求 的分布列;
的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
已知复数 (
( 为虚数单位)
为虚数单位)
(1)若 ,且
,且 ,求
,求 与
与 的值;
的值;
(2)设复数 在复平面上对应的向量分别为
在复平面上对应的向量分别为 ,若
,若 ,且
,且 ,求
,求 的最小正周期和单调递减区间.
的最小正周期和单调递减区间.
已知正四棱柱 的底面边长为2,
的底面边长为2, .
.
(1)求该四棱柱的侧面积与体积;
(2)若 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的大小.
所成角的大小.
已知函数 ,
, (其中
(其中 ,
, ),且函数
),且函数 的图象在点
的图象在点 处的切线与函数
处的切线与函数 的图象在点
的图象在点 处的切线重合.
处的切线重合.
(Ⅰ)求实数a,b的值;
(Ⅱ)若 ,满足
,满足 ,求实数m的取值范围;
,求实数m的取值范围;
如图,F1,F2是离心率为 的椭圆
的椭圆
C: (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线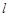 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 是否存在点M,使以PQ为直径的圆经过点F2,若存在,求出M点坐标,若不存在,请说明理由.
已知 ,数列
,数列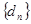 满足
满足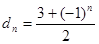 ,数列
,数列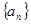 满足
满足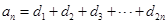 ;又知数列
;又知数列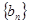 中,
中,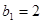 ,且对任意正整数
,且对任意正整数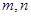 ,
,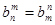 .
.
(Ⅰ)求数列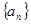 和数列
和数列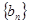 的通项公式;
的通项公式;
(Ⅱ)将数列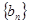 中的第
中的第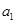 项,第
项,第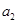 项,第
项,第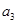 项,……,第
项,……,第 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列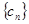 ,求数列
,求数列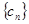 的前
的前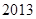 项和.
项和.