已知椭圆C: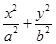 =1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=
=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c= b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
(1)求椭圆C的方程;
(2)若直线l1的斜率为-1,求△PMN的面积;
(3)若线段MN的中点在x轴上,求直线MN的方程.
(本小题满分10分)设f(x)=x3-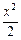 -2x+5.
-2x+5.
(1)求f(x)的单调区间;
(2)当x∈[1,2]时,存在f(x)<m成立,求实数m的取值范围.
 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。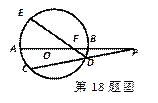
(本小题满分12分)
已知定义在 上的函数
上的函数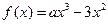 ,其中
,其中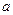 为大于零的常数.
为大于零的常数.
(Ⅰ)当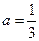 时,令
时,令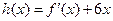 ,求证:当
,求证:当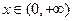 时,
时,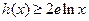 (
( 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数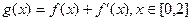 ,在
,在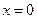 处取得最大值,求
处取得最大值,求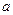 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式及
的通项公式及 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中 ,求
,求 的前
的前 项和.
项和.
(本小题满分12分)
如图, 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
,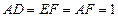 .
.
(Ⅰ)求四棱锥 的体积
的体积 ;(Ⅱ)求证:平面
;(Ⅱ)求证:平面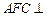 平面
平面 ;
;
(Ⅲ)在线段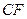 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,并说明理由.
,并说明理由.