如图，已知E是平行四边形ABCD对角线AC上的点，连接DE．
（1）过点B在平行四边形内部作射线BF交AC于点F，且使∠CBF=∠ADE（要求：用尺规作图，保留作图痕迹，不写作法与证明）
（2）连接BE，DF，判断四边形BFDE的形状并证明．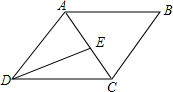
已知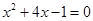
，求代数式
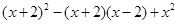的值．
解不等式组：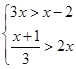
．
如图，△ABC中，∠ACB=90°，延长AC到D，使得CD=CB，过点D作DE⊥AB于点E，交BC于F．求证：AB=DF．
对于平面直角坐标系xOy中的点P和线段AB，给出如下定义：在线段AB外有一点P，如果在线段AB上存在两点C、D，使得∠CPD=90°，那么就把点P叫做线段AB的悬垂点．
（1）已知点A（2，0），O（0，0）
①若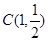
，D（1，1），E（1，2），在点C，D，E中，线段AO的悬垂点是______；
②如果点P（m，n）在直线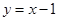
上，且是线段AO的悬垂点，求
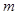的取值范围；
（2）如下图是帽形M（半圆与一条直径组成，点M是半圆的圆心），且圆M的半径是1，若帽形内部的所有点是某一条线段的悬垂点，求此线段长的取值范围．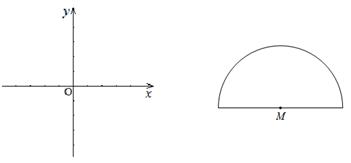
已知，点P是△ABC边AB上一动点（不与A，B重合）分别过点A，B向直线CP作垂线，垂足分别为E，F，Q为边AB的中点．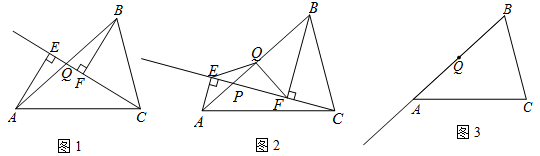
（1）如图1，当点P与点Q重合时，AE与BF的位置关系是，QE与QF的数量关系是；
（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；
（3）如图3，当点P在线段BA的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．