(本小题满分10分)已知函数 (其中
(其中 为正常数,
为正常数, )的最小正周期为
)的最小正周期为 .
.
(1)求 的值;
的值;
(2)在△ 中,若
中,若 ,且
,且 ,求
,求 .
.
已知动圆 过点
过点 ,且与
,且与 圆
圆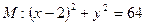 相内切.
相内切.
(1)求动圆 的圆心的轨迹方程;
的圆心的轨迹方程;
(2)设直线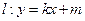 (其中
(其中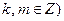 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D
,D ,与双曲线
,与双曲线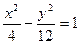 交于不同两点
交于不同两点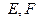 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知函数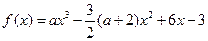 。
。
(1)当 时,求函数
时,求函数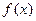 的极小值;
的极小值;
(2)试讨论函数 零点的个数。
零点的个数。
已知数列 满足
满足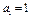 ,
, ,(
,( ,
,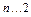 ).
).
(1)求证:数列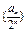 是等差数列;
是等差数列;
(2)若数列 的前
的前 项和为
项和为 ,且
,且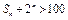 恒成立,求
恒成立,求 的最小值.
的最小值.
如图,在直三棱柱ABC-A1B1C1中,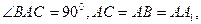 E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
|
(3)在(2)的条件下,求二面角A1-AG-E的大小