已知动圆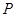 与圆
与圆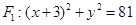 相切,且与圆
相切,且与圆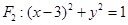 相内切,记圆心
相内切,记圆心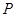 的轨迹为曲线
的轨迹为曲线 ;设
;设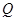 为曲线
为曲线 上的一个不在
上的一个不在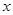 轴上的动点,
轴上的动点,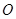 为坐标原点,过点
为坐标原点,过点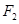 作
作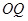 的平行线交曲线
的平行线交曲线 于
于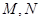 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究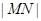 和
和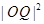 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记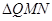 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
如图,在△ABC中,B= ,AC=2
,AC=2 ,cosC=
,cosC= .
.
(1)求sin∠BAC的值;
(2)设BC的中点为D,求中线AD的长.
如图,A,B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
如图所示,在四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形.
(1)将四边形ABCD的面积S表示为θ的函数;
(2)求S的最大值及此时θ角的值.
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c= .
.
(1)若sinC= ,求sinA的值;
,求sinA的值;
(2)设f(C)= sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.