一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间有如下组对应数据:
| x |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
| y |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
(1)画出散点图;
(2)求月总成本y与月总产量x之间的回归直线方程.
已知10只狗的血球体积及红血球的测量值如下:
| x |
45 |
42 |
46 |
48 |
42 |
35 |
58 |
40 |
39 |
50 |
| y |
6.53 |
6.30 |
9.25 |
7.50 |
6.99 |
5.90 |
9.49 |
6.20 |
6.55 |
7.72 |
x(血球体积,mm),y(血红球数,百万)
(1)画出上表的散点图;(2)求出回归直线并且画出图形。
以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
| 销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
| 年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 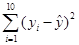 ;
;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算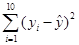 ; (3)比较(1)和(2)中的残差平方和
; (3)比较(1)和(2)中的残差平方和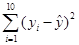 的大小.
的大小.
一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程
在7块并排、形状大小相同的试验田上进行施化肥量对水稻产量影响的试验,得数据如下(单位:kg)
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程