设函数 (a为实数).⑴若a<0,用函数单调性定义证明:
(a为实数).⑴若a<0,用函数单调性定义证明: 在
在 上是增函数;⑵若a=0,
上是增函数;⑵若a=0, 的图象与
的图象与 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数
 的解析式.
的解析式.
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+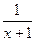 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
已知命题 :方程
:方程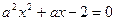 在[-1,1]上有解;命题
在[-1,1]上有解;命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
(12分)如图,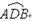 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线 l与曲线C相交于不同的两点M、N,且M在D、N之间,设
l与曲线C相交于不同的两点M、N,且M在D、N之间,设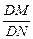 =λ,求λ的取值范围.
=λ,求λ的取值范围.
双曲线 (a>1,b>0)的焦距为2c,直线
(a>1,b>0)的焦距为2c,直线 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线 的距离之和s≥
的距离之和s≥ c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.