如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°, ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.

如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
求证:平面A B1D1∥平面EFG;
求二面角 的正切值。
的正切值。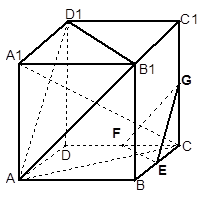
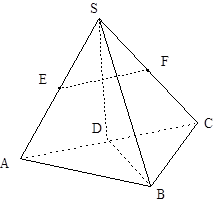
如图:在三棱锥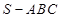 中,已知点
中,已知点 、
、 、
、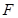 分别为棱
分别为棱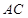 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若 ,
,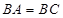 ,求证:平面
,求证:平面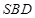 ⊥平面
⊥平面 .
.
已知直线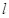 经过直线
经过直线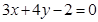 与直线
与直线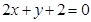 的交点
的交点 ,且垂直于直线
,且垂直于直线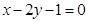 .
.
(Ⅰ)求直线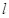 的方程;
的方程;
(Ⅱ)求直线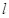 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积
焦点在x轴上的双曲线过点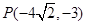 且点
且点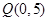 与两焦点的连线互相垂直。
与两焦点的连线互相垂直。
(1)求此双曲线的标准方程;
(2)过双曲线的右焦点倾斜角为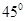 的直线与双曲线交于A、B两点,求
的直线与双曲线交于A、B两点,求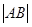 的长。
的长。
某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?