已知直四棱柱 的底面
的底面 为正方形,
为正方形, ,
, 为棱
为棱 的中点.
的中点.
(1)求证: ;
;
(2)设 为
为 中点,
中点, 为棱
为棱 上一点,且
上一点,且 ,求证:
,求证: .
.
如图, 在空间四边形SABC中, 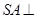 平面ABC,
平面ABC, 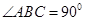 ,
, 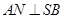 于N,
于N, 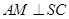 于M.
于M.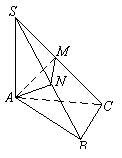
求证:①AN^BC; ②平面SAC^平面ANM
下面三个图中,右面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在左面画出(单位:cm).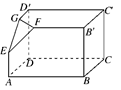
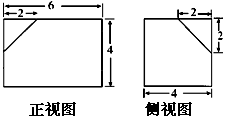
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
已知圆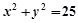 ,
, 内接于此圆,
内接于此圆,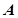 点的坐标
点的坐标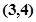 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)若 的重心是
的重心是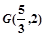 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若直线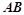 与直线
与直线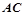 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线 的斜率为定值.
的斜率为定值.
如图,AB是过椭圆左焦点F的一弦,C是椭圆的右焦点,已知|AB|=|AC|=4,∠BAC=90°,求椭圆方程.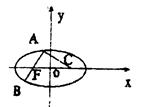
求与双曲线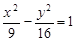 有共同渐近线,并且经过点 (-3,
有共同渐近线,并且经过点 (-3, )的双曲线方程.
)的双曲线方程.