完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )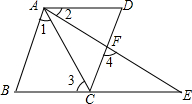
如图,已知点A、B、C、D在同一直线上,①BE∥AF,②∠E=∠F,③CE=DF,④ BD=AC,请选择其中的三个作为条件,一个作为结论,组成一个真命题,并给出证明.(只需写一种)我选择 作为条件, 作为结论.(填序号)
证明:
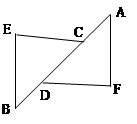
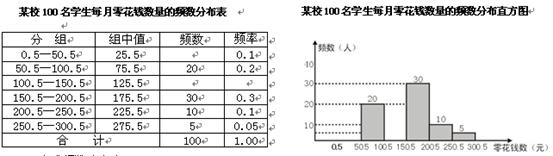
未成年人思想道德建设越来越受到社会的关注.某青少年研究机构随机调查了某校100学生每月花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,根据调查数据制成了如下的频数分布表(部分空格未填),并绘制成下面的频数分布直方图.请你思考并回答下列问题:完成频数分布表;
补全频数分布直方图;
研究认为应对消费200元以上的学生提出勤俭节约的建议,试估计应对该校1800名学生中约有多少名学生提出该项建议?
当n=0,1,2,3,4时,代数式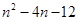 的值都是负数吗?请通过计算说明.由此你是否得出结论:对于所有的自然数n,代数式
的值都是负数吗?请通过计算说明.由此你是否得出结论:对于所有的自然数n,代数式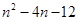 的值都是负数?若不是,请举例说明理由.
的值都是负数?若不是,请举例说明理由.
解方程: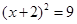
x2-3x+2=0
2010年1月1日,全球第三大自贸区——中国—东盟自由贸易区正式成立,标志着该贸易区开始步入“零关税”时代,广西某民营边贸公司要把240吨白砂糖运往东盟某国的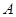 、
、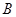 两地,先用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往
两地,先用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往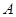 地的运费为:大车630元/辆,小车420元/辆;运往
地的运费为:大车630元/辆,小车420元/辆;运往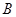 地的运费为:大车750元/辆,小车550元/辆.
地的运费为:大车750元/辆,小车550元/辆.求两种货车各用多少辆;
如果安排10辆货车前往
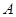 地,其余货车前往
地,其余货车前往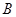 地,且运往
地,且运往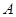 地的白砂糖不少于115吨.请你设计出使总运费最少的货车调配方案,并求出最少总运费.
地的白砂糖不少于115吨.请你设计出使总运费最少的货车调配方案,并求出最少总运费.